1.经验内容 我们现在得出了如下所述的经验内容的观念。我们说a的逻辑内容(或推论类)是指从a推出的所有陈述的类。因此,我们可以暂时先考虑把从。推出的所有观察陈述(或“基本陈述”,参见下面)的类叫做a的经验内容。 但是,这个尝试性的观念现在不起作用。因为,我们最感兴趣的是一个解释性的一般理论的经验内容;但是,单从这样一个理论是推不出观察陈述的。(从“一切乌鸦都是黑的”我们不可能推出任何像“现在这里有一只黑乌鸦”这样的观察陈述;尽管我们确实能推出“现在这里没有白乌鸦”。) 正因为这样,所以在定义经验内容时,我转而求助于这样的观念:一个理论告诉我们的观察事实越多,它禁止的这种事实也越多——就是说,和它不相容的可观察事实越多。[2]于是,我们就可以说,一个理论的经验内容是由那些和该理论相矛盾的观察陈述或基本陈述的类决定的(并且等同于这个类)。 和理论t相矛盾的一个基本陈述可以称做t的一个“潜在证伪者”。如果利用这个术语,我们便可以说,t的经验内容由它的潜在证伪者的类构成。 “经验内容”这个名字可正当地用于这个类,其理由可从以下事实看出:每当两个经验的(即非形而上学的)理论t1和t2的经验内容的量度ECt(t1)和ECt(t2)的关系使得 (1) ECt(t1) ≤ECt(t2) 成立时,它们的逻辑内容的量度的关系也将总是使得 (2) Ct(t1)≤Ct(t2) 成立;对于内容相等的情形,类似的关系亦成立。 现在转到“基本陈述”这个概念上来,我现在想改进对我在《科学发现的逻辑》(尤见第28和29节)中所称的“基本陈述”的讨论。为了命名一类陈述(真的或假的),我曾引入了“基本陈述”这个术语,在我们讨论中,可假定这类陈述具有无可置疑的经验性质。“无可置疑的”,这里是指,我们准备按照我们可能碰到的最挑剔、最讲究精确的经验主义者的要求来限制基本陈述的类,假如这些要求在精确性上并不比我们自己的(客观主义的)最低要求更低的话。这些要求是:(1)基本陈述陈述了(正确地或错误地)在某个足够狭窄的时空区域里的可观察事实(现象)的存在。(2)一个基本陈述的否定一般将不是基本的。对一些简单的基本陈述(例如:“在我书房里现在有一只成年的丹麦种大狗”)的例子,可以认为它们的否定是基本的;而大多数基本陈述(例如:“我书房里现在有一只蚊子”)的例子,它们的否定由于一些显而易见的理由而不能认为是基本的。(3)当(且仅当)两个基本陈述的合取在逻辑上一致时,这合取才总是基本的。(因此,每当一个陈述和它的否定都是基本的时候,它们的合取将总是非基本的。)我们可以从一类在其他场合可接受的基本陈述中挑出那些非复合陈述(“相对原子”陈述;试比较《科学发现的逻辑》第38节)。于是,如果我们愿意的话,我们就可以从这些陈述出发,并像下述那样构成一类新的基本陈述。(i)我们不承认相对原子基本陈述的任何否定是基本的。(ii)就基本陈述的一切合取都是一致的而言,我们承认它们都是基本的。(直觉地看,一致性似乎是一个必要的要求,采纳它便大大简化了继起理论的各种表述,但是,只要我们从证伪者类中排除掉不一致的陈述,我们就可以不管这个要求。)(iii)我们不承认任何复合基本陈述的否定,不承认基本陈述的合取以外的任何复合。 最后这种排斥可能看起来稍嫌严格:但是,我们的目的不是承认一切经验陈述都是基本的——甚至一切关于可观察事实的陈述也不都是基本的:我并不在乎把像“在我的书房里要么有一条成年的丹麦种大狗,要么有一匹成年的设德兰矮种马”这种复合观察陈述排斥出基本陈述的类,虽然不想把它们排除出经验陈述的类。因为,虽则我们旨在保证一切基本陈述都显然是经验的,我们并不打算保证相反的情形——一切明显经验的陈述(甚或一切观察陈述)都是“基本的”。 把基本陈述的否定(或几乎一切基本陈述的否定)排除出基本陈述的类以及把基本陈述的析取和条件句排除出这个类的目的是:我们并不希望承认像“如果这房间里有一只乌鸦,那么它是黑的”或者“如果这房间里有一只蚊子,那么它是一只疟蚊”这样的条件陈述。这些陈述无疑是经验陈述;但是从这里阐述的知识论观点来看,它们不具有理论的检验陈述的性质,而是具有例示陈述的性质,因此,它们意义不大,也不怎么“基本”;这里阐释的知识论认为,一切理论的经验基础都有待检验;或者换句话说,都有待尝试加以反驳。 这里可能值得提一下,“基本陈述”这个术语里的“基本的”这个词似乎已把我的一些读者引入了歧途。我使用这个术语有如下所述的一段历史。 在使用“基本的”和“基本陈述”这些术语以前,我利用了“经验基础”这个术语,用它意指所有那些可以起检验理论的作用(即作为潜在证伪者)的陈述的类。我引入“经验基础”这个术语,部分地是为了从反面强调我的论点:我们理论的经验基础远不是坚实的;应把它比作沼泽而不是硬地。[3] 经验主义者通常相信,经验基础由绝对“给定的”知觉或观察“材料”构成,科学可以建立在这些“材料”之上,犹如建立在岩石上一般。相反,我指出,表面的经验“材料”总是根据理论作的解释,所以它们总受到一切理论的假设性质或猜测性质的影响。 我们称做“知觉”的那些经验是一些解释——我认为这些解释是指对我们在“感觉”时发现自己置身于其中的那个总的情境的解释——这种见解当归于康德。这常常被笨拙地表述为:知觉是对通过感官给予我们的东西的解释;从这种表述中产生了一个信念,认为必定存在一些终极的“材料”,一些未经解释(因为解释必须是对某种东西作的,还因为不可能无穷地倒退)的终极材料。但是,这个论证没有考虑到(如康德所提出的那样)解释过程至少部分地是生理学的,因此,永远不会存在我们经验到的未作解释的“材料”:这些未作解释的“材料”的存在因此是一种理论,而不是一个经验事实,至少不是一种终极的或“基本的”事实。 可见,不存在未作解释的经验基础;构成经验基础的检验陈述不可能是表达未作解释的“材料”的陈述(因为不存在这样的材料),而只是陈述关于我们物理环境的可观察的简单事实的陈述。当然,它们是根据理论解释的事实,可以说它们是浸泡在理论之中。 就如我在《科学发现的逻辑》(第25节结尾)中指出的那样,陈述“这里有一杯水”不可能由任何观察经验来证实。理由是出现在这个陈述中的全称词项(“杯子”、“水”)是倾向性的:它们“标示呈现某种类规律变化的物体”。[4] 这里就“杯子”和“水”所说的也适用于一切描述性的全称词项。 经验主义者如此钟爱的那只著名的受责备的猫(我也觉得猫惹人喜欢)是一个比杯子和水理论性更强的实体。一切词项都是理论词项,尽管一些比另一些理论性更强。(比起“已碎的”来,“可碎的”理论性或倾向性都更高,但前者也是理论性或倾向性的,就如前面第三章结尾处举例提到的那样。) 对这个问题持这样的观点,我们就有可能把含有高度理论性的词项的陈述纳入我们的“经验基础”,假如这些陈述是关于可观察事实的单称陈述的话;例如,像“这里有一只读数为一百四十五的电位计”或“这只钟的读数是三点三十分”这样的陈述。这仪器事实上是一个电位计这一点,不可能被最终确立或证实——就像我们面前盛有水的那个杯子不能最终确立或证实一样。不过,它是一个可检验的假说,我们在任何物理实验室里都可以很容易地检验它。 因此,每个陈述(或“基本陈述”)本质上仍然是猜想性的;但是,它是一个很容易检验的猜想。这些检验本身又包含了新的猜想性的和可检验的陈述,如此等等,以至无穷;如果我们试图用检验来确立什么东西,那么我们就会陷于无穷倒退。但是,像我在《科学发现的逻辑》中所解释的那样(特别是第29节),我们不会用这个程序确立什么东西:我们不想“证明”对什么东西的“验收”,我们仅仅批判地检验我们的理论,以便看看我们能否找到一个它的反例。 因此,我们的“基本陈述”决不是在“终极”的意义上成为“基本的”;它们只是在它们属于用来检验我们理论的那类陈述的意义上,才是“基本的”。 2.概率和检验的严格性 我们的检验的严格性能够客观地加以比较;如果我们愿意的话,我们也可对它们的严格性规定一个尺度。 在这个限定以及本附录后面的讨论中,我将在概率演算的意义上利用概率的思想;或者更确切地说,利用相对概率的思想: p(x,y), 它读做“对于给定的y,x的概率”。绝对概率的思想: p(x), 它读做“x的绝对概率”,这里将用相对概率来加以定义,它的显定义是 D(AP) p(a)=p(a,b)<—>(c)(Ed)(p(b,b)=p(c,d)—>p(a,b)=p(a,c))。 这里“(a)”是“对于每一个a”的缩写;“(Ea)”是“存在着一个a”的缩写;“<—>”是“当且仅当”的缩写;“……—>……”是“如果……那么……”的缩写。(后面我们还要用“&”作为“和”的缩写。)为了直观地解释D(AP),我们可以选择c的否定作为d。 相对概率p(x、y)的思想这里像在D(AP)中一样,将主要用作定义者。它本身又可用一个公理系统隐含地定义,就像在我的《科学发现的逻辑》(新的附录*Ⅳ和*V)中一样。那里给出的六条公理可以简并为三条,其中的一条A是一条存在公理,另外两条B和C是(“创造性的”[5])定义形式的公理: A (Ea)(Eb)p(a,b)≠P(b,b) 就是说,至少存在二种不同的概率。 B ((d)p(ab,d)=p(c,d))<—>(e)(f)(p(a,b)≤p(c,d)&p(a,e)≥p(c,e)≤p(b,c)&((p(b,e)≤p(f,e)&p(b,f)≥p(f,f)≤p(e,f))—>p(a,f)p(b,e)=p(c,e))) 公理B用p(x,y)定义乘积ab(读做“a和b”)。 C p(-a,b)=p(b,b)-p(a,b)<—>(Ec)p(b,b)≠p(c,b) 公理C用p(x,y)定义补-a(读做“非a”)。 对这三条公理,我们还可以添加三条(非创造性的或普通的)定义:上面用D(AP)定义的绝对概率p(a)的定义;布尔恒等式a=b的定义;和相对于b的n项的独立的定义。 恒等式定义如下: D(=) a=b<—>(c)p(a,c)=p(b,c) 我们认为如果所谓(相对于b的)“特殊乘法定理”适用于An集的2n-1个非空子集中的每一项,那么一个n个元素的集成n项的序列an=a1,…,an,是“n项独立的(相对于b)”。令ai,…,am为任何这种子集(或子序列)的元素;那么,如果An是n项独立的,则我们有 (m) p(ai…am,b)=p(ai,b)·p(ai+1,b)…p(am,b) 式中右边是m-i概率的乘积。在这些2n-1方程中,对应于An的2n-1非空子集,将存在n个无足轻重的方程(对于单元子集),因为对于m=i,我们的方程(m)退化为 (i) p(ai,b)=p(ai,b); 这就是说,每一单个元素不过是1项独立的(相对于每一个b)。因此,An的n项独立乃由2n-n-1个重要的方程定义。[6] 这个运用2n-n-1个方程的有点笨拙的定义可加以简化,为此引入“Indpn(a1,…,an;b)”的一个递归定义,它读做“a1,…,an是n项独立的(相对于b)”: D(Indp) (i)Indp1(a1;b),对于我们可能选择的任意的元素a1和b。 (ii)Indpn+1(a1,…,an+1;b),当且仅当 (a)Indpn(a1,…an;b); (b)Indpn(a1,…,an;(an+1b)); (c)p(ai,(an+1b))=p(ai,b),对于每一个元素ai(1≤i≤n)。 这里我们可以用 (b’) p(an+1,aj…amb)=p(an+l,b,)其中aj…am(对于j≤m≤n)是An的任何子集的元素的合取,取代(b)和(c)。 这些定义可以加强:对于一个无穷的理论,在最后的括号前,例如在(c)中插入一个仅仅在假设P(ai,b)≠0之下从(c)推出的方程 “&p(an+1,ai,b)=p(an+1,b)”,可能是合适的。 现在,我们可以转到检验的严格性的定义上了。 设h是有待检验的假说;设e是检验陈述(证据),b是“背景知识”,也即我们在检验该理论时认为(暂时地)没有问题的那一切东西。(b也可以包含初始条件性的陈述。)让我们先假定,e是h和b的一个逻辑推论(这个假定后面将要放宽),这样p(e,hb)=1。例如,e可以是从牛顿的理论h和我们对火星过去位置的知识(构成b之一部分)推出的一个关于火星的一个预言位置的陈述。 于是,我们可以说,如果我们把e作为h的一个检验,那么,在只给出b(没有h)时,e越不可几,解释为支持证据的这检验的严格性就越高;也就是说,对于给定的b的e的概率p(e,b)就越小。 定义检验e对于给定b的严格性S(e,b),主要有两种方法[7]。两者都从内容度量Ct出发。第一种方法把概率的补作为内容的度量Ct: (1) Ct(a)=1-p(a); 第二种方法把概率的倒数作为内容的度量: (2) Ct’(a)=1/p(a) 第一种方法提出了一个像S(e,b)=1-p(e,b)这样的定义,或者更好地表达为 (3) S(e,b)=(1-p(e,b))/(1+p(e,b)) 就是说,它建议我们用Ct度量检验的严格性,或者更好地用“正规化的”Ct(利用1/(1+p(e,b))作为一个正规化因子)来度量它。第二种方法提议我们只要用检验的内容Ct’,来度量它的严格性: (4) S’(e,b)=Ct’(a,b)=1/p(e,b)。 现在我们来推广这些定义,为此我们放宽e应逻辑地从h和b推出这个要求,甚或放宽下列更弱的要求: p(e,hb)=1就是说我们现在假定存在某种概率,p(e,hb),它可能等于1,也可能不等于1。 这意味着,为了得到(3)和(4)的一个推广,我们在这两个公式中都用更一般的项“p(e,hb)”代替“1”。因此,我们得出了下面两个解释为理论h的支持证据的(对于给定的背景知识b)检验e的严格性的推广定义。 (5) S(e,h,b)=(p(e,hb)-p(e,b))/(p(e,hb)+P(e,b)); (6) S’(e,h,b)=p(e,hb)/P(e,b)。 这些就是我们对作为支持证据的检验的严格性的度量。这两种度量之间没有选择余地,因为从一种到另一种的转移是保序的[8];就是说,两者都是拓扑不变的。(如果我们用Ct’和S’的对数[9]例如log2Ct”和log2S’代替Ct’和S’——以使这些度量成为加性的,情形同样如此。) 在定义了我们的检验的严格性的度量后,现在我们可以用同样的方法来定义理论h在b出现的条件下关于e的解释力E(h,e,b)(而且如果我们愿意的话,也可以类似方式定义h的确证度[10]): (7) E(h,e,b)=S(e,h,b); (8) E’(h,e,b)=S’(e,h,b)。 这些定义表明,对理论h的一次检验e越严格,理论h(关于某个被解释者e)的解释力就越大。 现在显而易见,一个理论的解释力的最大程度或者它的检验的严格性的最大程度乃取决于该理论的(信息的或经验的)内容。 因此,知识的进步或潜在增长的标准将是我们理论的信息内容或经验内容的增加;同时,是它们可检验性的增加,也是它们有关(已知的和未知的)现象的解释力的增加。 3.逼真性 这一节将进一步讨论和发展第十章第x和xi节的思想(这里假定读者已经读过它们)。 在塔尔斯基的真理理论中,“真理”是陈述的一个性质。我们可以用“T”标示某种人工的语言(对象语言;参见下面第5节)的所有真陈述的类。我们可以用 a∈T 表达(某种元语言的)断定:陈述a是真陈述类的一个成员,换句话说,a是真的。 我们在这里的首要任务是定义一个陈述。的真内容的观念,我们用“CtT(a)”标示它。这定义必须使得一个假陈述和一个真陈述都有真内容。 如果a是真的,那么a的真内容CtT(a)(或更确切地说,它的度量)将仅仅是。的内容的度量;也即 (1) a ∈T—> CtT(a)=Ct(a)式中我们可以像第2节的(1)一样,建立 (2) Ct(a)=1-p(a)。 假如a是假的,则正如已经提到过的那样,它仍然可以有真内容。因为,假定今天是星期一,那么陈述“今天是星期二”将是假的。但是,这个假陈述将蕴含一些真陈述,例如“今天不是星期三”或“今天或者是星期一或者是星期二”;它所蕴含的所有真陈述的类将是它的(逻辑的)真内容。换句话说,每个假陈述都蕴含一个真陈述类这个事实是把一个真内容赋予每个假陈述的基础。 所以,我们将把陈述a的(逻辑的)真内容定义为既属于G的(逻辑的)内容又属于T的那些陈述的类;因而我们也解释了它的真内容的度量CtT(a)。 为了在理论Ct或p(这里Ct(a)=1-p(a))的内部给CtT(a)观念下定义,我们可以应用各种方法。 最简单的方法或许是同意,在像p(a)或p(a,b)这样的表达式内,字母“a”、“b”等等不仅可以是陈述的名字(因而也是,例如,有限个陈述的合取的名字),而且也可以是陈述的类的名称(或者属于这些类的所有陈述的有限或无限的合取的名字),因此,我们也就同意用符号“t”[11](在像p(t)、P(a,t)或P(t,b)这样的语境之中)代替“T”,并把它看作是所考虑的语言系统(或陈述系统)的一切真陈述的(有限或无限的)合取。换句话说,我们把符号“t”用作变项“a”、“b”等等可能取的常值之一,并且同意以下述方式使用它: (3) t的推论类或逻辑内容是T。 然后我们定义一个新符号“aT”如下: (4) aT=avt我们从这个定义得出(用“「”标示“蕴含”即“从……推出……”」 (5) a 「aT从而还得出 (6) p(aaT)=p(a), (7) p(a,aT)p(aT)=p(aaT)=p(a)。我们还得出 (8) aT「x,当且仅当a「x&x∈T,式中“a「b”还是读做“b可从a推出(或者由a蕴含)”。因此,(8)的意思是:aT是a所蕴含的逻辑上最强的真陈述(或演绎系统)。因此,我们现在可以把a的真内容定义为aT的真内容,而它的度量CtT(a)现在可以定义如下: (9) CtT(a)=Ct(aT)=1-p(aT) 从(9)和(5)得出 (10) CtT(a)≤Ct(a)和 (11) 如果a∈T,那么aT=a,以及CtT(a)=Ct(a) 为了定义“Vs(a)”——即a的逼真性(的度量)——我们不仅需要a的真内容,而且还需要它的假内容——或者它的度量——因为我们希望把vs(a)定义为a的真内容和假内容之差异这类东西。但是,a的假内容或它的某种替代物的定义不是很简单的,因为存在这样的基本事实:了可以说是构成了一个推论类或内容(t的内容,参见上面的(3)),而我们系统的所有假陈述的类F却不是推论类。因为,虽则T包含T的一切逻辑推论——因为任何真东西的逻辑推论必定也是真的——但F并不包含所有它的逻辑推论:从一个真陈述只能推出真陈述,而从一个假陈述不仅能推出假陈述,而且也总能推出真陈述。 因此,按类似于“真内容”的方式来定义“假内容”,看来是行不通的。 为了得出a的假内容的度量CtF(a)的一个令人满意的定义,规定一些必需的定理是有益的: (i) a ∈T—>CtF(a)=0 (ii) a∈F—>CtF(a)≤Ct(a) (iii) 0≤CtF(a)≤Ct(a)≤1 (iv) CtF(contrad)=Ct(contrad)=1 式中“contrad"是自相矛盾的陈述的名字。所需要的定理(iv)应该和定理 CtT(tautol)=Ct(tautol)=0 加以比较和对照。式中“tautol"是一个重言陈述的名字。 (v) CtT(a)=0—>CtF(a)=Ct(a) (vi) CtF(a)=0—>CtT(a)=Ct(a) (vii) CtT(a)+CtF(a)≥Ct(a)(如果取“a”为,例如“contrad",则可看出这里用“≥”而不是“=”的理由;因为在这种情况下,我们根据(iv)和CtT(a)=Ct(t)得到CtF(a)=Ct(a)=1,但是,Ct(t)是最大真内容,它通常区别于零。在一个无限域里,Ct(t)=1-p(t)通常将等于1。) (Viii) CtF和CtT在下述意义上关于Ct是对称的:存在两种函数,f1和f2,以致 (a) CtT(a)+CtF(a)=Ct(a)+f1(CtT(a),CtF(a)) =Ct(a)+f1(CtF (a),CtT(a)) 就是说,f1关于CtT和CtF是对称的;因此,结果我们便得到 (b) CtT (a)=f2(Ct(a),CtF(a)) (c) CtF(a)=f2(Ct(a),CtT(a))。 在按这些方式定义“CtF(a)”的各种可能性中,以下定义是可取的,这里就采用这个定义:(12) CtF (a)=1-p(a,aT)=Ct(a, aT)这个定义满足我们的需要。对于所要求的定理(i)和(ii)来说,这是显而易见的;如果我们考虑以下定理,那么这对于其他所要求的定理来说,也变得很清楚: (13) CtF(a)p(aT)=p(aT)-(p(a, aT)p(aT))=p(aT)-p(a) 参见(7) =Ct(a)- CtT (a) 因此 (14) CtT(a)=Ct(a)-( CtF (a)p(aT))≤Ct(a)。 (15) CtF(a)=(Ct(a)- CtT (a))/P(aT)=(Ct(a)- CtT(a))/(1- CtT (a)) (16) CtT(a)p(a, aT)=p(a, aT)-(p(aT)p(a, aT))=p(a,aT)-p(a)=Ct(a)- CtF (a) 于是,我们就得到 (17) CtF(a)=Ct(a)-( CtT (a)p(a, aT))≤Cta (18) CtT(a)=(Ct(a)- CtF (a))/P(a,aT) 参见(iii) =(Ct(a)- CtF (a))/(1- CtF (a))见(15) 我们从(15)还得到(19) CtF (a)- CtT (a) CtF(a)=Ct(a)- CtT (a)从而还有 (20) CtT (a)+ CtF (a)=Ct(a)+ CtT(a) CtF (a) 所以,(17)表明(iii)得到满足,而(20)表明(v)、(vi)、(vii)和(viii)也都得到满足。(iv)的满足可以从p(contrad,t)=0得出。 这表明,对CtF (a)所提出的定义(12)满足一切我们所需要的定理。但是,我们所需要的定理之一(vii)可能显得不可满足:或许可以看到——尽管我们对(vii)作了评论——我们应该假定 (一) CtT(a)+ CtF (a)=Ct(a) 可以表明,方程(一)实际上决定了CtF:它将导致定义(我们不接受这个定义) CtF (a)=Ct(aT—>a)=1—p(aT—>a),式中“aT—>a”(或者,我们还可以写作“a<—aT”),是条件陈述“如果aT,那么a”或者“a,如果aT”。 把这个定义和我们的(12)相比较,或者换句话说,把Ct(a<—aT)和Ct(a,aT)相比较(后者就是我们的CtF (a)),或者把p(a<—aT)和p(a,aT)相比较,是很有意思的。 诚然,我们有 CtT (a)+Ct(a<—aT)=Ct(a),乍一看来,这似乎令人满意。 但是,让我们用“contrad"代替a: CtT (contrad)=Ct(t)=1-P(t),如我们已经看到的那样,这是我们体系中可得到的最大真内容;因为Ct(contrad)=1,所以我们得到Ct(a<—aT)=Ct(contrad<—t)=1-P(contradv-t)=p(t)。现在,虽然CtT (contrad)=Ct(t)完全无可非议——它显然是CtT(a)的一个令人满意的定义的推论,也显然是一切东西,因而包括‘都从一个自相矛盾的陈述推出这一事实的推论——但是,CtT(contrad)=p(t)的情形却并非如此;因为,这在大多数情况下会使得一个矛盾的假内容少于它的真内容,而我们本来期望一个矛盾的假内容至少等于它的真内容。 举个例子,设我们的论域是掷骰子;设t“3面朝上”;设p(t)为1/6。对CtF(a)=Ct(a<—aT)所提出的(但这里是被拒斥了的)定义在现在的论域里将导致这样的结果:一个矛盾陈述(像“6将面朝上并且不朝上”)的假内容CtF(contrad)将等于1/6,而它的真内容CtT (contrad)将等于5/6。可见,一个矛盾陈述的真内容将大大超过假内容,而这显然是违反直观的。正因为这样,所以才要采用我们需要的定理(iv);这个定理导致 CtT (a)+ CtF(a)>Ct(a)的情形。 从这一切可以看到,我们所需要的定理(iv)可由下面两条高度直观的定理代替:(iv,a) CtF (contrad)=常数, (iv,b) CtF(contrad)≥CtT (contrad)。 附带指出,事实上我们每每得到(21) CtF (a)-Ct(a<—aT)= CtF(a) CtT (a),这看来有点令人惊讶。但是,它只是下面更为一般的公式的一个直接推论: (22) p(a<—b)-P(a,b)=Ct(a,b)ct(b),这个公式我在好多年前就得出了,为的是要表明,一个条件陈述“a,如果b”(或者陈述“如果b,那么a”)的绝对概率通常超过某个陈述a(对于另一个给定陈述6)的相对概率。 (因此,可以说,公式(22)把朝向左边的箭头“<—”和逗号“,”进行了比较,并计算了条件概率对于相对概率的永恒非负的超出量: Exc(a,b)=p(a<—b)-p(a,b)。) 定义了真内容和假内容的度量之后,我们现在可以来定义Vs(a)即a的似真度了。就我们仅对相对值感兴趣而言,我们能够用 CtT(a)-CtF(a)=p(a,aT)-P(aT) 作为定义者。如果我们对数值感兴趣,那么最好用一个正规化因子去乘它,并且用(p(a,aT)-p(a,)/(p(a,aT)+ P(aT)作为定义者。因为,我们希望下面的所需要定理得到满足。 (i) VS(a)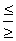 Vs(b) <—>、CtT(a)-CtF(a) Vs(b) <—>、CtT(a)-CtF(a)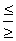 CtT(b)- CtF (b); CtT(b)- CtF (b); (ii) -1≤VS(a)≤ VS(t)≤1; (iii) VS(tautol)=0; (iv) Vs(contrad)=-1; 因此,我们得到 (v) -1=Vs(contrad)≤b(a)≤+1; (vi)在一个Ct(t)可以成为1的无限域中,Vs(t)应该也能成为1。 这里应该指出,Ct(t)=1-p(t)将取决于我们论域的选择。甚至在一个潜在无限的论域里,它也可能小于1,就如下述例子所表明的那样:设我们的论域包含互斥可能的一个可数无限集a1,a2,……,并设p(a1)=1/2,p(a2)=1/4,p(a3)=1/8,p(an)=1/2n;此外,再设这些可能性中只有一个得到实现:t=a1;那么, Ct(t)= 1/2。 因此,为了作数值计算,最好是用一个正规化的形式去代替P(a,aT)- P(aT);我们选取正规化因子1/(P(a, aT)+ P(aT));就是说,如上所述,我们定义:(23) Vs(a)=(p(a,aT)-p(aT))/(p(a, aT)+p(aT))。 我们现在得到: (24)如果 a ∈T,那么 Vs(a)= CtT(a)/(1+p(aT))= Ct(a)/ (1+p(a)),(25) Vs(tautol)=0, 和 (26)Vs(coytrad)=-l。 还存在其他各种可能的定义。例如,我们可以引人其他正规化因子,如CtT(a)、Ct(a)或者 CtT(a)+CtF(a)。我认为,这些不会导致Vs(a)的恰当定义,倒是会导致像“真值度”这类观念的定义。 4.数值的例子 在讨论一些数值例子——这些例子必须取自于那些把概率运用于靠碰运气取胜的游戏的理论或者统计理论——之前,我希望先对纯粹容度和概率理论中的数值作些一般的论述。 除了那些我们能用一般方式(或者借助在投骰子时的等概率假定,或者借助统计假说)度量概率的概率论应用而外,我看不出有把数值(除了0和1)赋予我们的概率或容度的量度的可能。就此而言,纯粹概率论和纯粹容度理论很像欧几里得几何:欧几里得几何里没有加以定义的实际单位。(巴黎单位米的定义无疑是超几何学的。)我们不必因为纯粹概率论或客度理论不提供实际的数值(除了0和1)而担心。因此,我们的地位在许多方面更像拓扑学,而不是度量几何。[12] 现在来谈数值例子。我将区分两种类型。 (l)普通掷骰子型的例子。这里,如果比如说4朝上,而我们猜的是5朝上,那么,我们认为,这不比猜6朝上更好,也不更坏。(这里是在离真实更近或更远的意义上使用更好或更坏的。) (n)我们的猜测离开真实之距离有一种度量的例子。我们能够用下述假设来表示这一例子:如果事实上4朝上,则5将朝上(或3将朝上)这个猜测或命题就把6将朝上(或2将朝上)这个命题同真理隔开了;由于这个缘故,因此如果a=6,则aT就将是 6v5v4,而不是 6v4(或者 aT=2v3v4)。[13] 这里和下面,“a=6”或“a=6v4’都用于表达“a=6将朝上”或“a=6v4将朝上”,等等。 我们取几颗同类的骰子。 我首先计算类型(i)的三个例子。 (1) a=6; b=4; b=t 我们有: aT= 6v4; p(a,aT)= 1/2; p(aT)=1/3 Vs(a)= 1/5 (2) a=5; b=4; b=t 我们有aT=5v4。这计算和结果同。情形(1)相同。 (3) a=6v5; b=4; b=t我们有 aT=6v5v4;P(a,aT)=2/3;P(aT)=1/2 VS(a)= 1/7 我们现在可以把这些和类型(ii)的三个相应的例子加以比较。差别在于aT的计算。 (1’) a=6;b=4; b= t 我们有: aT =6v5v4;p(a, aT)=1/3;p(aT)=1/2 Vs(a)=-1/5 (2’) a=5;b=4; b=t 我们有: aT= 5v4;p(a,aT)=1/2;p(aT)=1/3 Vs(a)= 1/5 (3’) a=6v5; b=4; b=t 我们有: aT=6v5v4; p(a,aT)=2/3;p(aT)= 1/2 Vs(a) =1/7 。 我现在再增加两个准确猜测的例子: (1”) a=6; b=6; b=t; Vs(a)=5/7 (2”) a=6v5;b=6; b=t; Vs(a)=1/2 。 于是,我们看到,逼真度可能随着a的容度而增加,随着a的概率而减少。 5.人造语言和形式化语言 人们常说,塔尔斯基的真理理论只适用于形式化语言系统。我认为这种说法不正确。众所周知,塔尔斯基的真理理论需要一种带某种程度人为性的语言——一种对象语言;它还需要区分对象语言和无语言,而这种区分有一定程度的人为性。然而,虽然通过把某种谨慎引人日常语言,我们使它丧失了“自然”性,带上了人为性,但是,我们不一定使它形式化:虽然每种形式化语言都是人造的,但并非每种服从某些规定的规则,或者建基于多少清楚地表述的规则的(所以是“人工的”)语言都一定是完全形式化的语言。在我看来,承认存在一整套不同程度上人为的但不是形式化的语言,是相当重要的,对于真理论的哲学评价尤为重要。 6.对逼真性的一个历史注释(1964年) 这里要对逼真性和概率之间的混淆的早期史作些评论(作为对第十章第xiv节的补充)。 (1)简言之,我的命题如下所述。我们所掌握的最早的说法明确地运用类真或逼真的观念。后来,“类真”变得模棱两可了:它获得了附加的意义诸如“像真的”或“或然的”或“可能的”,因此,在有些场合就不清楚是指哪种意思了。 在柏拉图那里,由于他的极关重要的模仿或模拟理论,这种模棱两可变得很明显:正如经验世界模仿理念的(真)世界一样,经验世界的说明或理论或神话也(似乎)“模仿”真理,因而只是“类似真理”;或者,把同样这些词句按它们的其他意思来译,这些理论不是可证明的、必然的或者真实的,而只是或然的、可能的或者(一定程度上)是似乎真实的。 这样,柏拉图的模拟理论便为(那时已流行的)错误的和引人人歧途的“类真的”等于“或然的”的等式提供了类似哲学基础的东西。 亚里士多德使一个附加的意义变得相当突出:“或然的”=“频繁地出现的”。 (2)为了提供一点细节,我们先看看《奥德赛》的19,203这段:足智多谋的俄底修斯告诉珀涅罗珀(她没有认出他来)一个包含了一点儿真实因素的虚假故事;或者像荷马所说的那样,“他使得许多谎言像真理一样”(“etumoisinhomoia")。在《神谱》的27f中重复了这句话:奥林匹斯的缪斯,这些宙斯的女儿们,对赫希俄德说:“我们懂得怎样撒许多谎,说得像真理一样;但是,我们也懂得怎样说真理(aletheia),如果我们愿意的话。” 这段话也很有意思,因为这段话里,etumos和alethes都作为“真实”的同义词出现。 包含短语“etumolsin homoia"的第三段是《神谱》的713,这里狡猾受到赞扬(就像在《奥德赛》里一样),把谎言说得像真的一样的能力被说成是神授的(也许暗中指《神谱》中的缪斯):“你应该用神一般的内斯特的如簧巧舌把谎言说得像真话一样。” 和这些段落有关的一件事是,它们全都和我们今天所称的“文学批评”有关。因为,这是个“讲故事”的问题,而这些故事是(和听起来是)像真的似的。 在色诺芬那里可以看到非常相似的一段话,色诺芬本人就是个诗人,也许还是第一个文学批评家。他引入了(DKB35)术语“eoikota”来代替“homia”。也许在提到他自己的神学理论时,他说:“我们可以猜想,这些东西同真理相似”(eoikomtoisetu—moisi;亦见前面第217页)。 这里我们又获得了一个短语,这个短语同一个术语一起明确地表达了逼真性(不是概率)的观念,这个术语(我已把它译成“我们可以猜想”)源出于doxa(“意见”),而doxa这个术语在巴门尼德那里和巴门尼德以后起了十分重要的作用。(这个术语也出现在色诺芬的最后一行即B34中,这一行前面已在第37和217页上引过,用于同“saphes”即“确实真理”相对比。) 接下去的一步是重要的。巴门尼德的B8,60使用了eoikota(“相似的”或“类似的”),而没有明确地提到“真理”。我认为,还是像在色诺芬那里一样,意思是“像真理似的”,我前已按此翻译了这段话(“完全像真理”;参见前面第16页)。我的主要论据是它和色诺芬B35相似。这两段话都是说凡人的意见或猜想(doxa),两段话都说了一些相当赞同它的话;两段话都显然意味着,这种相当“好的”意见实际上并非真实叙述。尽管有这些相似性,巴门尼德的话常常还是被译成“或然的和可能的”(参见前面第338页上的注①)。 这一段是很有意义的,因为它和柏拉图的《蒂迈欧篇》中的一段重要的话(27e-30c)密切相关。在这一段里,·柏拉图从巴门尼德区分“始终现存和从不生成的东西”与“始终生成着和从不现存的东西”开始(27e-28a);他附和巴门尼德说,第一种东西能被理性认识,而第二种“是意见和非理性感觉的一个对象”(亦比较前面的第235页)。 从这出发,他继续解释道,变化和生成着的世界(ouranos或cosmos:28b)是由造物主创造的一个摹本或类似物(eikon),它的原型或范型是永恒不变的现存的存在。 在巴门尼德那里,从范型到摹本的过渡相当于从“真理之路”到“似然之路”的过渡。我前面已引用过后一种过渡(第16页),它包含术语“eoikota”,而后者和柏拉图的“eikon”,即和“类似真实”或“类似现存东西”相关;从中我们或许可以得出结论:柏拉图把“eoikota”读作“类似(真实)的”而不是“或然的”或“可能的”。 然而,柏拉图还说过:在作为类似真实的东西时,摹本不可能确实地被知道,对它我们只能有意见,而这种意见是不确实的、“可能的”或者“或然的”。因为他说,对范型的说明是“经久不变的、不可动摇的、不可反驳的和战无不胜的”(29b-c),而“对(仅仅是)范型摹本的类似性的东西的说明将……(只)具有类似性;因为,像现存相对生成一样,真理相对(纯粹)信念也是这样。” 正是这一段引入了在不完全确实信念或部分信念的意义上的相似性或或然性(eikota),而同时又把它和逼真性联系起来。 这一段结束时,这种向“似然之路”的过渡又发出了一个回响:正像女神允诺巴门尼德给出一个“完全像真理”的说明,以致再不能提供更好的说明一样(前面第16页),我们在《蒂迈欧篇》(29d)中读到:“如果我们能提供一个说明,它在相似性(eikota)上比其他说明都好,记住[我们]……是人类这种创造物,接受一种似真的说法(eikotamuthon)是与我们相称的……那么,我们应该满足”。(对这一点,“苏格拉底”回答道:“妙极了,蒂迈欧!”) 应当指出,饶有兴味的是,这个关于“类真性”和“相似性”(即“或然性”)之间非偶然的含糊解释的介绍并没有使柏拉图后来在《克力锡亚斯篇》(107e)中避免在“类真说明”的意义上使用这个术语。因为,鉴于前文,这段话应读为:“就天上的和神性的事物而言,我们应当满足于一种类真度很低的说明,但是,我们仍应仔细地检验凡人的说明的精确性。.” (3)除了柏拉图使用"eikota"(和类似性质的术语)时这种系统的和无疑故意的含糊之外,除了范围广泛的形形色色意思明确的用法之外,还存在着广泛的意思根本不明确的用法。在柏拉图(和亚里土多德)那里,不同用法的例子是:它用于同“可证明的”和“必然的”相反的意思;宦用于表达“仅次于确实性”。它也常用作“肯定”、“当然”或者“这在我看来似乎完全正确”的同义语,尤其用作对话中的插人语。它在“或许”的意义上使用;它甚至在“频繁出现”的意义上使用;例如,在亚里士多德的《修辞学》的2,25,8里:“……或然的东西(eikos)不是不可避免地会出现,而只是在大多数场合下会出现的东西……” (4)我打算用另一段文字批判作为结束,这段话在亚里士多德的《诗学》(1456a,18,18,和1461b,25,29)中出现了两次,在第一次出现时,他把它归诸诗人安喀松。“也许不可能的事情要发生了。”或者更明确些说,虽然略欠文采:“不可能的事情要发生了,这像是真的。” 补充注释 自从1960年写这篇(现已扩大了的)第五章的附录以来,我已读过了查尔斯.H.卡恩的最令人敬佩的书《阿那克西曼德和希腊宇宙论的起源》(1960年)。卡恩正确地强调了关于自然的早期思辨的“本质上的统一性”(第5页),并指出阿那克西曼德思想的框架至少直到柏拉图的《蒂迈欧篇》为止始终统治着后继者的宇宙论。我认为他的强调是重要的,因为它矫正了我本人对这些后继理论新奇性的强调。但是,在我看来,我的论点,即新奇性是批判性论争的结果,似乎把这两种观点都包括了进去:显然既有统一性又有新奇性。 这里,对卡恩和我都感到非常重要的阿那克西曼德的地球自由悬浮理论,或许我可以再补充一点。我提出过,这个理论很可能是阿那克西曼德批判泰勒斯的结果。但是,我觉得很清楚,它也是对《神谱》中的一段话(720-725)的一个批判的反响。这段话明确提出,地球和围绕着它的宇宙各部分是等距离的:因为这里说在地球下面的地狱跟地球的距离与地球上方的天堂跟地球的距离一样远。(亦比较《伊利亚特》8,13—16;《伊尼特》vi577。)这段话还强烈地使人感到,我们能够画一幅图,在这幅图中,如果天体被设想为一种球,那么,地球就将占据阿那克西曼德指定的位置。[14]
[1] 这些附录中讨论的各个技术性问题特别和本书第10章有关。它们以前没有发表过。 [2] 参见《科学发现的逻辑》第31、34节。卡尔纳普接受了这个思想:尤见他的《概率的逻辑基础》一文,1950年,第406页,以及他的《符号逻辑》[SymbolischeLogik],第2版,1960年。第21页。 [3] 尤见我的(科学发现的逻辑)的第30节最后一段。 [4] 《科学发现的逻辑》,第25节,第95页;新附录*x,(1)到(4),第422-426页。亦见例如本书第1章(第iv、v节)和第3章(第6节最后6段)。 [5] 关于“创造性的”和“非创造性的”定义的讨论,可参见例如P.萨珀斯的《逻辑导论》[Introductionto Logic]1957年,第153页,还有我的论文《概率演算中的创造性和非创造性定义》[Creativeand Non-Creative Definitions in the Calculus of Probsbility]载《综合》[Synthese],1963年,第2期,第167页以后。 [6] 试比较例如W.费勒的《概率论及其应用导论》[AnIntroduction to ProbabilityTheory and its Applications]第1卷,第2版,1957年,第117页。顺便指出,我们可以把空子集等同于其惟一元素为-(a,-a)的单元子集,因为这个元素是(相对于b)绝对地独立的,即相对于任何集An独立的。因此,我们得到了2n个方程,它们的n+1涉及单元类,并且是很平常的。 [7] 参见《科学发现的逻辑》第83节注。②(第270页) [8] 参见《科学发现的逻辑》第404页。 [9] 同上书,第402-406页。 [10] 同上书,第400-402页。 [11] 注意,“t”现在不是用来标示“重言式”;对重言式,我们后面还将引入符号“tautol”。(因为了很可能是不可公理化的,所以这种使用“t”的方法可以说等于把a,b,…,t,…解释为演绎体系(而不是解释为陈述);参见塔尔斯基:《逻辑,语义学,元数学》第342页及以后,和第382页上谈到S.马祖凯维茨的地方)。 [12] 这里假定的概率论在《科学发现的逻辑》的附录*iv和v中阐发了;亦见本附录上面的第2节。 [13] “6v5v4”,和“6v4”在这里是“或6或5或4朝上”和“6或4朝上”的缩写。 [14] 卡恩引了《伊利亚特》8,13—16。虽然他提到了《神谱》,但并没有涉及《神谱》的720—5(也许因为在某些稿本中第721-725行缺失抑或由于其他疑问?),这可以解释为什么他这样(第82页)说到《神谱》727ff等:“想画一幅图来配这样一种描述,是没有希望的。”
|